数学で高得点を取るために(二次試験対策)
- 著者
- 北海道大学医学部医学科に在籍のT講師。札幌のトップ高校出身で、医学部には首席で合格しています。理数系科目だけでなく、文系科目にも対応でき、レベルの高い指導に定評があります。気さくな人柄で、現在、シニアの本部教室で3名の生徒を担当しています。
- 内容
- 一般的に言われる「数学はパターンである」の真意について述べられており、数学で高得点を取るための方法論として、とても参考になる内容です。
1.「大学への数学」との出会い
僕がそれからのパートナーである「大数」と出会ったのは今から四年前……高校二年生の時のリラ冷えの春だった。
その日は朝からいつも僕を起こしてくれる飼い猫のハナの姿が見えず、リビングにいってみると、ハナの朝ご飯はあるが僕の朝ごはんがきれいさっぱり消えていた。不可解に思いながら・・・(中略)、帰り道、朝食にありつけずお腹を減らした僕は、鼻腔を刺激する芳醇なにおいに連れられて本屋へと足を向けた。
そこで僕は運命的に出会った。
「大学への数学」
この本なしに僕の受験を語ることはできないだろう――
などと駄文を綴っていても東京出版のダイマにしかならないので、ここでは僕が、受験勉強を通して学んだちょっとしたテクについて語ろうと思う。
本当は勉強の仕方とか、大学受験の際の心構えとかを書こうとしたが、あまり一般向けの話にならなかったためである。授業は聞かないで問題集をひたすら解いては、解答集で答え合わせをする方が建設的である、なんていった不真面目な話ばかりになるからである。
2.「数学はパターンである」という言葉の真意
本題に入るとしよう。
「数学の問題演習というのは何の意味があるのだろうか」と考えたことはないだろうか。社会や理科と違って、問題演習と全く同じ問題が出ることは数学にはありえない。また、公式を覚えていれば数学のあらゆる問題は理論上解けるはずである。したがって、数学において問題演習は必要ない、無駄なことではないのだろうか。
往々にして、この問いに対する答えは、「一度解いた問題と全く同じ問題が出なくとも、似たような問題は出るから」である。
それゆえに「数学はパターンである」という言葉が横行する。
解いたことがある問題に近い問題ならば、難問でも解けるだろう、ということだ。そういう考え方のもと僕たちは数学の問題集をやってきて、今もやっているのだろう。
学校の教員や塾の教師に散々、耳にタコができるほど言われてきたであろう、この「数学はパターンである」という言葉。この文章では僕の考えるこの言葉の真意、本意について書いていこうと思う。
抽象的な話をしてもいいのだが、それだとこれを読み終えたときに得たものが判然としなくなるのは目に見えているので、ここではとりあえず分かりやすい「極限」という分野を例にとって話をしてみる。
受験生諸兄の中には聞いたことがある人も多くいるだろうが、「○○の極限を求めよ」という頻出問題の解法というのは、大別すると五つしかない。すなわち、
- ①見たまんま
- ②公式
- ③ハサミうち
- ④微分の定義
- ⑤区分求積
である。
まあこのうち二つや三つの解法にまたがるものも存在はするが、この五つを超えるものがないというのが重要だ。
せっかくなので、一つずつを細かく見ていく。
①見たまんま
字面だけでは何を言っているかわからないと思うが、僕もこれをどう表記するか迷ったものである。要するに、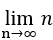 とか
とか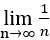 などといった公式ですらない基礎的な極限のことである。こういった問題は数式さえ出してしまえば極限を求めるのは簡単なため、その数式を出すまでが難しいものが普通である。
などといった公式ですらない基礎的な極限のことである。こういった問題は数式さえ出してしまえば極限を求めるのは簡単なため、その数式を出すまでが難しいものが普通である。
②公式
例えば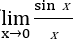 などの三角関数系の極限とか
などの三角関数系の極限とか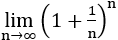 である。意外と忘れがちなので念頭においておくといい。こういったタイプのものは、公式とそれ以外の部分に式を分解してから極限を求めるとミスが少なくなる。
である。意外と忘れがちなので念頭においておくといい。こういったタイプのものは、公式とそれ以外の部分に式を分解してから極限を求めるとミスが少なくなる。
③ハサミうち
いわずと知れたハサミうちの定理を使用して極限を求めるタイプの問題である。定義の段階で求めるxに範囲が示されている場合などはハサミうちの場合が多い。また、どう考えてもこの条件で極限を求めることは不可能と感じる問題や、考え方のとっかかりもつかめない問題はハサミうちでしか解けないことがザラである。
ここまでが順当な極限の求め方であり、ここからは少々ひねくれた問題となってくる。
④微分の定義
ずばり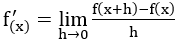 である。極限は数Ⅲの範囲なので学習するのは普通高校三年生である。が、これは微分の話なので数Ⅱ、つまり高校二年生で学習する範囲である。これを習った際は「何の意味があるんだこの定義は」と思い、そのまま忘却する人が多いため、極限と微分の定義が結びつかない人が多く、これがからむ極限の問題は難問になりやすい。
である。極限は数Ⅲの範囲なので学習するのは普通高校三年生である。が、これは微分の話なので数Ⅱ、つまり高校二年生で学習する範囲である。これを習った際は「何の意味があるんだこの定義は」と思い、そのまま忘却する人が多いため、極限と微分の定義が結びつかない人が多く、これがからむ極限の問題は難問になりやすい。
とはいえ、例えば極限を求める式を分解していったらいい感じに上記の式になって微分したら答えが出る。例えば平均値の定理と微分の定義を利用してハサミうちで落としこむ。などなど意外と微分の定義を使う問題は多い。極限を解くうえで可能性の一つとして頭の片隅には入れておきたい。
⑤区分求積
これは極限の後にやった人も多いと思うが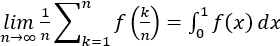 とか、
とか、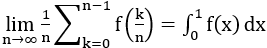 とかのことである。これの厄介なところは、この二つの公式を覚えれば区分求積を使いこなせるというわけではないことである。
とかのことである。これの厄介なところは、この二つの公式を覚えれば区分求積を使いこなせるというわけではないことである。
区分求積という言葉は、普段なら積分を使って求める数式によって囲まれた面積を、限りなく横幅が狭い帯を無限に足し合わせることによって求める、という考え方そのものを表している。したがって、公式など無限にあるため、状況に応じて必要な公式を考えなければならないのである。論理を理解していればそう難しいものでもないが、理解してなければほぼ不可能だろう。
さしあたって、上記の二式でいえば、左式の総和の範囲のnがn-1に変わっても右式に変わりがないということを説明できるかどうかで理解度をはかることもできるだろう。厄介な問題ではこれを使ったうえでハサミうちをする、なんて問題も見たことがある。ともあれ、区分求積を使うかどうかは判断がしやすいので 言ってしまえば楽である。
もっとも、Σが出てきて区分求積だと思ったら、総和を必死に計算して極限自体は普通に出す、なんて問題もあるわけだが。
3. 解法の可能性を羅列できるように
ここまで五パターンの極限の解法について述べてきたが、まあ何が言いたいのかというと、これから極限の問題を解く際に、初めからこの五パターンを念頭においた方が、当たり前だが効率がいいということだ。
このことから言えることは、「数学はパターンである」という言葉を完全に実践するなら、単にこの問題は一度見たことがあると考えるだけに留めず、自らの頭の中で問題パターンを分類し表にするまでやる必要があるということだ。そうすれば問題を解く段階になって、解法の可能性を頭の中に何個か羅列することができる。すると、今まで手も足も出なかった問題の糸口が見えてきて答えまでの道順をたどることができるようになるのだ。
大学入試の二次試験の数学というのは、高校入試やセンター試験と違い、難しい問題を数問、たっぷりの時間とともに出題してくる。こういった問題を解くためには様々な解法を試さなければならない。そう考えれば、上述のように解法の可能性を羅列できるようになることがどれほどのアドバンテージたりうるのかが真に理解できるだろう。
4. 問題の解法を分類し表にする
今回は極限を例にとってみたが、こういったようにある程度分類しやすい解法というのは結構ある。例えば、ベクトルにおける面積の出し方だったり、帰納法の使い方だったり。
もちろん、今あげたのは一例である。解法の種類は書こうと思えばいくらでも書けるが、今回はこの辺で筆をおいておこうと思う。自分で問題を解いていく中で、新しい解法の分類を見つけてほしいからだ。
これから数学の二次試験の対策をしようという人にはぜひ、問題を解く前に解法の可能性を羅列してみてほしい。それは確実に高得点に結びつくからだ。
そのためにも自分の中で問題の解法を分類し表にするということを、これからは心がけてみてほしい。
-
- O講師の
数学偏差値40台から
北海道大学医学部に合格した勉強法 - 数学では、何に重点をおいて学習すれば良いかが明確に語られており、数学の学習に不安のある生徒にとっては、とても役立つ内容だと思います。偏差値40台からでも十分挽回できます。
- O講師の
-
- O講師の
北大英語で8割が取れる勉強法 - 大学入試で、英語を得点源にする勉強法がわかりやすく書かれています。南高で実テ1位はなかなか取れません。英語が伸び悩んでいる生徒にはとても参考になると思います。
- O講師の
-
- U講師の
物理が苦手な状態から、北大総合理系物理重点1位を取った勉強法 - 物理で得点できない生徒が多い中、物理学習において、何に気をつけて学習していけば良いのかが丁寧に述べられています。物理で受験する生徒にはとても参考になると思います。
- U講師の
-
- U講師の
追試を受けるほどの状態から
数学を得意・武器とした勉強法 - 数学学習において一番大切なのは、「基礎」。著者の一番伝えたいことが、何度も語られています。生徒の皆さんには、単に言葉として受けとめるのではなく、模試の見直し等で実感してほしいと思います。
- U講師の
-
- 鈴木講師の
勉強を楽しむ - とにかく、勉強は楽しみながら進めることが大切で、それができれば自ずと成績も伸びてくる、というのをモットーにしている講師です。いろいろと誘惑の多い現在、勉強よりも楽しいことがいっぱいあって、勉強はとかく辛いものになりがちですが、自身の勉強の楽しみ方が教科毎に述べられています。
- 鈴木講師の
-
- N講師の
北大物理で9割近くの点数で安定する勉強法 - 物理で高得点を取るための方法が、簡潔明瞭に述べられています。
- N講師の
-
- O講師の
センター生物からみた過去問の重要性と共通テスト対策 - 来年の1月からセンター試験に変わる大学入学共通テストが実施されますが、その対策の仕方や二次試験対策までが丁寧に述べられています。
- O講師の
-
- O講師の
受験数学で「頭打ち」から抜け出すために必要な考え方と勉強法 - 数学で飛躍すべき方法論が具体的に述べられています。
- O講師の
-
- H講師の
物理を0から得意科目に - 一般的に取っ付きにくい物理の学習において、大切にすべきこと、解き直しの重要性、オススメの問題集などが丁寧に述べられています。
- H講師の
-
- T講師の
化学を得意に - 化学が大得意と言うだけあって、化学を学習する上でおさえるべきポイントが、単元別に明確に述べられています。化学に不安を感じている生徒、伸び悩んでいる生徒は、ここに書かれていることを、今日から実践して欲しいと思います。
- T講師の
-
- E講師の
「自分との闘い」と「物理」 - 医学部受験に向けての甘えや不安の克服、そして、物理の得点を大幅にアップさせた勉強法が、具体的に語られています。
- E講師の
-
- M君の
難関私大入試の英語の勉強法 - 慶應大学はじめ難関私大入試のための英語の勉強法が、丁寧に述べられています。また、使用教材についても、余すところなく紹介されています。
- M君の
-
- T講師の
数学で高得点を取るために
(二次試験対策) - 一般的に言われる「数学はパターンである」の真意について述べられており、数学で高得点を取るための方法論として、とても参考になる内容です。
- T講師の
-
- M君の
おすすめの化学の勉強方法 - 化学の勉強法、得点源にするための方法論が、丁寧に述べられています。化学が苦手な生徒、伸び悩んでいる生徒には、とても参考になる内容だと思います。
- M君の
-
- M君の
物理学習に対する心構え - 物理はどのように勉強していけば良いのか、何を意識して取り組めば良いのかが、問題集の取り組み方なども含めて、わかりやすく書かれています。物理を苦手にしている生徒、あるいは、苦手にはしていないが伸び悩んでいる生徒には、とても参考になると思います。
- M君の
-
- Uさんの
偏差値33からの大逆転 - これだけ遅くからの勉強で、北大に現役合格した話を聞いたことがありません。中学の復習からスタートした大学受験への取り組みが、詳細に述べられています。目標を諦めかけている生徒、もうダメだと思っている生徒には、とても参考になります。
- Uさんの
-
- K・Yさんの
数学を武器にする
(トップ高校での数学学習法) - 公立のトップ高校での数学の取り組み方・克服の仕方や、普段の学習方法などが説明されています。特に、授業の大切さ、復習の必要性が述べれられています。トップ高校の生徒は必読です。
- K・Yさんの
-
- M君の
数学学習上のヒントについて - 数学対策について、実践的な内容がちりばめられており、難関大学の数学対策にはとても参考になる内容です。特に、検算の大切さ、難問が出題された場合の対処法は必読です。おすすめの参考書も記載があります。
- M君の
-
- Sさんの
英語の長文読解のヒントについて - 英語の長文読解のヒントだけではなく、英語の学び方についても、やさしく丁寧に触れられています。高校生の方だけではなく、中学生の方にも参考になると思います。
- Sさんの
-
- H君の
数学のすゝめについて - 数学の得点アップのための方法論が丁寧に述べられています。
計算力対策、公式の覚え方は、納得です。高校生の普段の学習シュケジュールはとても参考になります。受験で数学が武器になります!
- H君の
-
- K君の
現代文の勉強法について - 評論文対策についての勉強法が丁寧に述べられています。国語の点数は伸びないと諦めかけている高校生には必読です。
- K君の
-
- K君の
化学の勉強法のヒントについて - 化学は暗記だけの科目ではありません。参考書は複数、問題集は一冊を使う!化学が苦手な高校生だけでなく、化学が得意な高校生にも参考になります。
- K君の
-
- A君の
物理学習のヒントについて - 効率の良い物理の学習法について丁寧に述べられています。物理が苦手な高校生、物理が嫌いな高校生は是非読んでみて下さい。問題集についても触れられています。
- A君の
-
- T講師の
人工知能の研究について - 大学入試には直接結びつきませんが、大学院での研究テーマである「人工知能」の内容がわかりやすく書かれ、最近の応用分野にも触れられています。人工知能に興味を持つ生徒がどんどん出てきて、大学進学を目指して欲しいと思います。
- T講師の
- お気軽にご相談ください。お電話お待ちしております。
-
各種お問い合わせ(日祝除く10~21時)
0120-973-595
